Misura del calore specifico

Luciano Troilo, Creato con GeoGebra

Con i rispettivi cursori scegliere:

• Il  materiale e la massa del campione di metallo che poniamo nel beaker. (Il campione deve essere ricoperto da una sufficiente quantità d'acqua.)

• La  quantità d'acqua posta nel calorimetro e la sua temperatura iniziale.

• Cliccare su "reset" per inizializzare la simulazione.

• Spostare il cursore "Fornello" su "acceso"

• Aspettare che l'acqua bolla

• Spostare il campione dal beaker nel calorimetro (poi si può spegnere il fornello)

• L'acqua del calorimetro comincia a scaldarsi fino a raggiungere una temperatura di equilibrio t_e

Per comodità riportiamo in ordine le grandezze misurate:

ma=..............      (massa dell'acqua versata nel calorimetro)

mc = .............     (massa del campione)

me= 30 g           (equivalente in acqua del nostro calorimetro)

t1= ..............     (temperatura iniziale dell'acqua contenuta nel calorimetro)

t2=...............    (temperatura del campione prima dell'immersione nel calorimetro = temperatura dell'acqua

                          nel beaker.  Leggere la temperatura nel momento in cui si sposta il campione dal beaker al calorimetro)

te = ..............     (temperatura finale di equilibrio tra acqua e campione immerso nel calorimetro)

 

Se abbiamo avuto cura di chiudere bene il coperchio del calorimetro possiamo affermare che tutto il calore perso dal campione metallico è stato assorbito dall'acqua nel calorimetro, quindi usando la relazione fondamentale della termologia Q = c m ∆t possiamo ricare la formula per calcolare il calore specifico del metallo (vedi teoria):

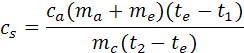
dove ca è il calore specifico dell'acqua che in queste misure si può porre uguale a 1cal/(g°C)

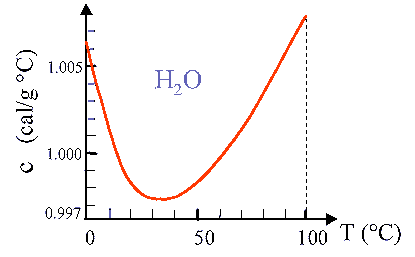
Si riporta un esempio

Misura del calore specifico del ferro

ma = 100g  

mc = 100g    

t1 = 8°C    

t2 = 100°C   

 

Sul termometro del calorimetro leggiamo la temperatura d'equilibrio: te = 15°C

Applicando la formula si ottiene: cs del ferro =0.107 cal/(g°C)

 

Calore specifico di alcuni metalli

Sostanza	cal/(g × °C)	J/(kg   × °C)
Alluminio	0.21	896
Argento	0.057	239
Rame	0.092	385
Zinco	0.096	389
Piombo	0.031	129
Ferro	0.108	450
Stagno	0.057	239
Bronzo	0.091	380
Invar (lega di acciaio al 36% di Ni)	0.11	460
Ottone	0.091	380
Oro	0.031	129

MISURA DEL CALORE SPECIFICO DEI METALLI
 

Il calore specifico di un corpo è una costante che dipende solo dalla sostanza di cui è costituito il corpo. Quantitativamente esso è espresso dalla formula:

Il calore specifico è il rapporto tra la quantità di calore scambiata da un corpo conseguentemente ad una variazione di temperatura ∆t e il prodotto della massa per la variazione della temperatura.

Il calorimetro delle mescolanze è lo strumento usato per determinare i calori specifici  delle sostanze. Si tratta di un thermos con le pareti rivestire da un materiale isolante in modo da rendere minima la dispersione di calore verso l'esterno. Il coperchio ermetico è dotato di due fori che consentono l’introduzione di un termometro e di un agitatore per uniformare la temperatura del liquido contenuto all’interno.
Nel calorimetro sia contenuta una massa d’acqua m_a ad una temperatura t₁. Se mettiamo nel calorimetro un oggetto di metallo di massa m_c ad una temperatura t₂> t₁ , dopo un certo tempo, viene raggiunta la temperatura di equilibrio t_e.
La quantità di calore ceduta dall’oggetto di metallo m_c è:

dove c_s è il calore specifico del metallo. In assenza di dispersioni Q₂ dovrebbe essere uguale alla quantità di calore Q₁ assorbita dalla massa di acqua m_a avente calore specifico c_a:

pertanto il calore specifico del metallo è determinabile dalla relazione:
 

In realtà un calorimetro non è un contenitore perfettamente ideale, perché, anche se è ben isolato verso l’esterno partecipa allo scambio termico assorbendo una parte del calore in esso scambiato. Per descrivere questa proprietà del calorimetro si utilizza l’equivalente in acqua m_e, detta anche massa equivalente, cioè quella massa di acqua che, nelle stesse condizioni di scambio termico, assorbirebbe la stessa quantità di calore che viene realmente assorbita dal calorimetro. Se è noto l’equivalente in acqua, un calorimetro può essere considerato ideale ammettendo che contenga una quantità di acqua ma + me; di conseguenza, la relazione precedente deve essere riscritta nel seguente modo:

Si introduce nel calorimetro una massa m_a di acqua alla temperatura t₁. Si riscalda una massa d'acqua m_c  su un fornello, dopo averne misurato la temperatura t₂  si versa nel calorimetro. Si misura, dopo adeguato mescolamento, la temperatura di equilibrio t_e. Ragionando come nel caso precedente e considerando uguali i calori specifici dell’acqua alle due diverse temperature, ricaviamo