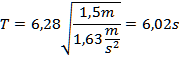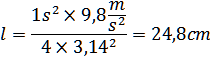EXPERIMENTAL PHYSICS

 

simple pendulum

Loading applet, be patient

Luciano Troilo, created with GeoGebra

ACTIVITY

FIRST TEST

Maintain fixed the length and changing the amplitude of the oscillation. Record the results in a table.

The period increases, decreases or remains constant?

Click here to download and see an example

 

SECOND TEST

Maintain fixed the amplitude of the oscillation and changing the length. Measure the period. Record the result in a table.

Check the hypothesis.

  1. The period of oscillations is proportional to the square root of the pendulum length.

 

Use an Excel spreadsheet to analyse the results.

Click here to download and see an example

 

THEORY

Laws of simple pendulum 

A pendulum is a weight suspended from a pivot so that it can swing freely.

 

Small-angle approximation

If it is assumed that the oscillation's angle is much less than 1 radian the period of swing is approximately the same for different size swings: that is, the period is independent of amplitude. This property, called isochronism, is the reason pendulums are so useful for timekeeping. Successive swings of the pendulum, even if changing in amplitude, take the same amount of time:

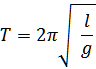
where T is the period of swing, g is the acceleration due to  gravity and l is the lenght of the pendulum.

 

 

1-Isochronism: for small swings, the period of swing is approximately the same for different size swings: that is, the period is independent of amplitude

 

2-For pendulums of length L the period of oscillations is the same regardless of the mass M of the suspended particle .

 

3-For pendulums of length L the period of oscillations is proportional to the square root of the length.

 

4-For pendulums of length L the period of oscillations varies according to the inverse of the square root of the local gravity acceleration

 

 

PROBLEMS/EXERCISES

1)Calculate the period of oscillation of a simple pendulum, 1.5m long, on the moon.

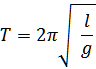
I dont have the acceleration due to gravity on the moon. I searched a value on the internet. I found g = 1, 63 m/s 2. So:

2) Find the length of the pendulum which has a specified period. We use this formula:

Example: build a pendulum that beats the second (i.e. , we need to find the length of the pendulum that has the period to 1 sec). In Italy g=9.8m/s 2.

 

3)Measure the acceleration due to gravity in a certain place of the Earth

example:
these are the results of measurements of 10 complete oscillations made from a 3 m long pendulum: T1=35.2s,T2=34.6s, T3=34.4s. Calculate the acceleration due to gravity. Calculate the average of the measurements, then divide by 10

 

    Then calculate g:

 

THE END

Go to home